Расчёт балки на прогиб
(прогиб металлического бруса (трубы) круглого или квадратного сечения)
Прогиб балки под нагрузкой
Графоаналитический расчет прогиба металлического бруса (трубы) круглого или квадратного профиля
В данном разделе рассматриваются четыре вида нагрузок и четыре различных формы сечения
металлической балки - квадратная труба, круглая труба, квадратный сплошной брус, круглый сплошной брус.
Расчитаны (приведены расчетные формулы): момент сопротивления, момент инерции, изгибающий момент, максимальная нагрузка (допустимая нагрузка), прогиб (изгиб).
С помощью графоаналитического расчета выполняется подбор геометрических параметров металлической балки круглого или квадратного профиля под заданную максимальную нагрузку.
Для указанных профилей момент сопротивления W и момент инерции J определяются по следующим зависимостям:
- для бруса с поперечным сечением квадратной формы (вариант 1):
W
= h03 / 6,
J = h04 / 12;
- для бруса с поперечным сечением круглой формы (вариант 2):
W
= 0,0982 · d03,
J = 0,0481 · d04;
- для трубы квадратного профиля (вариант 3):
W
= [ h04 -h14 ] / 6 · h0,
J = [ h04 - h14 ] / 12;
- для трубы круглого профиля (вариант 4):
W
= 0,0982 · [ d04 - d14 ] / d0,
J = 0,0491 · [ d04 - d14 ].
Допустимая нагрузка Fmax, изгибающий момент М и прогиб у в наиболее опасном сечении определяются по формулам:
- для варианта 1:
M1
= F · L,
F1max = s· W / L, y
= F · L3 / [ 3 · E · J];
- для варианта
2:
M2
= F · L / 2, F2max = 2 ·s·
W / L, y = F · L3 /
[ 8 · E · J ],
F = q · L (q - погонная нагрузка);
- для варианта 3:
M3
= F · L / 4, F3max = 4 ·s·
W / L,
y = F · L3 / [ 48 ·
E · J ];
- для варианта 4
M4
= F · L / 8, F4max = 8 ·s·
W / L, y = 5 · F · L3
/ [ 384 · E · J ],
F = q · L.
Брус - это тело, у которого один из трех размеров, определяющих его габариты, (длина) значительно больше двух остальных.
При рассмотрении процессов растяжения или сжатия брус может называться стержнем, при изгибе - балкой.
Стержень называют тонкостенным, если отношение ширины стенок к толщине состаляет более 5...10. Поперечное сечение тонкостенного стержня называют его профилем.
Для выбора оптимального сочетания заданной нагрузки, допустимой нагрузки, величины прогиба, материала и размеров балки, момента инерции, момента сопротивления, изгибающего момента
используем графоаналитический метод и сформируем систему номограмм.
|
С-ма номограмм №1.
Диапазон
параметров:
F1max
= 60 ... 300 kgf
F2max
= 120 ... 600 kgf
F3max
= 240 ... 1200 kgf
F4max
= 480 ... 2400 kgf
L
= 2 ... 5 m
F
= 30 ... 1600 kgf
h0
= 50 ... 75 mm
h1
= 20 ... 63 mm
d0
= 55 ... 85 mm
d1
= 20 ... 70 mm
W
= 6 ... 54 cm3
s=700
... 3000 kgf/cm2
E·105
= 4 ... 21 kgf/cm2
J
= 30 ... 174 cm4
С-ма
номограмм №2.
Диапазон
параметров:
F1max
= 10 ... 400 kgf
F2max
= 20 ... 800 kgf
F3max
= 40 ... 1600 kgf
F4max
= 80 ... 3200 kgf
L
= 1 ... 2.5 m
F
= 40 ... 1800 kgf
h0
= 35 ... 65 mm
h1
= 20 ... 53 mm
d0
= 40 ... 70 mm
d1
= 20 ... 56 mm
W
= 1 ... 36 cm3
s=
700 ... 3000 kgf/cm2
E·105
= 4 ... 21 kgf/cm2
J
= 11 ... 138 cm4
С-ма
номограмм №3.
Диапазон
параметров:
F1max
= 20 ... 500 kgf
F2max
= 40 ... 1000 kgf
F3max
= 80 ... 2000 kgf
F4max
= 160 ... 4000 kgf
L
= 0.5 ... 1.1 m
F
= 50 ... 1800 kgf
h0
= 25 ... 55 mm
h1
= 15 ... 46 mm
d0
= 30 ... 70 mm
d1
= 15 ... 49 mm
W
= 1 ... 36 cm3
s=
600 ... 3000 kgf/cm2
E·105
= 2.5 ... 21 kgf/cm2
J
= 3 ... 138 cm4
Перевод единиц:
1 кгс/см2 = 98,0665 кПа
1 кгс = 9,80665 Н |
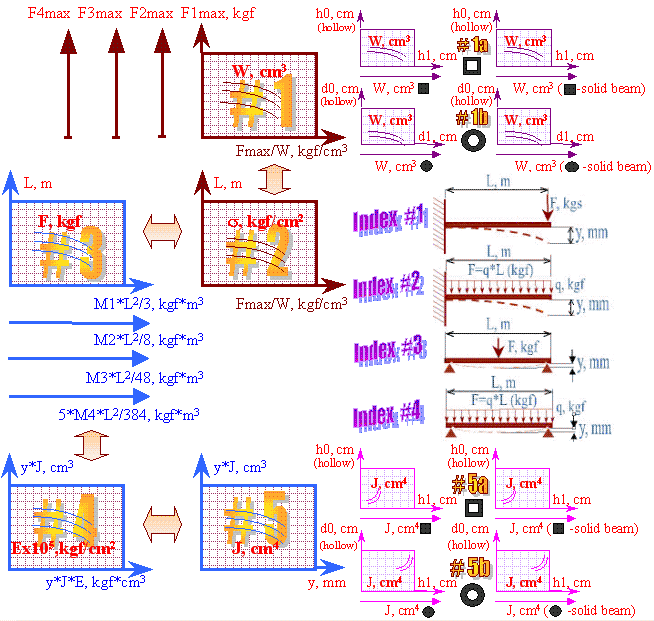
Параметры расчета балки на прогиб (изгиб)
Fmax
- максимально допустимая нагрузка, кгс (kgf);
W
- момент сопротивления, см3 (cm3);
s
- допускаемое напряжение при изгибе, кгс/см2
(kgf/cm2);
L
- длина балки, м (m);
F
- усилие в опасном сечении, кгс (kgf);
E
- модуль упругости, кгс/см2 (kgf/cm2);
J
- момент инерции, см4 (cm4);
у
- перемещение в опасном сечении при
изгибе (прогиб), мм (mm);
h0
- наружный размер бруса, см (cm);
h1
- внутренний размер бруса, см (cm);
d0
- наружный диаметр трубы, см (cm);
d1
- внутренний диаметр трубы, см (cm).
Перечисленные параметры выделены на рисунке красным цветом. |
Порядок графоаналитического расчёта балки на прогиб
1. Находим на графиках известные значения параметров (рассчитанные или начальные - в первом приближении).
2. Неизвестные значения остальных параметров находим с использованием смежных номограмм.
Примеры - расчет балки на прогиб
Пример 1. Турник - стальная труба (сталь
20Х) длиной L=1 м с наружным диаметром d0=34 мм и внутренним
d1=26 мм с нежестко закреплёнными
концами. Масса спортсмена - F=100 кг. В данном
случае имеем третий вариант нагружения с
усилием 100 кгс.
С помощью номограммы
№ 1b определяем момент сопротивления
для данного профиля - W=2,7 см3.
Допускаемое напряжение при изгибе для
данного материала трубы принимаем s=1500 кгс/см2.
На номограмме № 2 находим Complex А=15100 кгс/см3.
На номограмме № 1 определяем для третьей схемы
нагружения значение предельного усилия F3max :
F3max = 158 кг.
Далее на номограмме
№ 3 определяем промежуточное
значение - М33·L2/4 = 33 кгс*м3.
Поскольку для третьей схемы нагружения М33·L2/4
= y·J·E, находим на номограмме № 4 значение Complex B = 17 см5
(значение модуля упругости
стали принимаем Е=20·105кгс/см2). С
помощью номограммы № 5b определяем момент
инерции для данного профиля - J = 4,5 см4.
Итак, для данного момента инерции J значение
перемещения (прогиб) у = 26 мм.
В результате данного расчёта на пргиб получили
следующий результат.
Предельная нагрузка - 158 кг. Турник под весом спортсмена 100 кг прогнётся на 27 мм.
Проведём расчёт для заданных условий с
помощью инженерного калькулятора. В результате точного расчёта получим:
W = 2,54 см3;
F3max=152,4 кгс; J=4,32 cм4; у=24 мм.
|
Пример 2.
Рама с
закреплёнными на ней боронами имеет массу
900 кг. Вся конструкция консольно
закреплена на нескольких балках
квадратного профиля. Длина консоли 3 м.
Выполнить расчет на прогиб балки.
Определить количество балок и параметры сечения.
|
Пример 3. Сколько мешков
массой 50 кг каждый можно
равномерно сложить на две трубы
квадратного сечения с наружным
диаметром 55 мм и внутренним - 40 мм,
размещённых на двух опорах с
расстоянием между ними 2,7 м? Определить прогиб труб, если уложить четвёртую
часть от этого количества мешков. Задан
материал труб с характеристиками - s=1300кгс/см2,
E=2x106 кгс/см2. |
|
Принимаем количество балок равное четырём.
Параметры профиля - h0 = 70 мм, h1 = 50 мм.
Тогда
на каждую балку приходится нагрузка 225 кгс от веса рамы с боронами (1 вариант нагружения). Выбираем
материал со следующими параметрами -
s=2200 кгс/см2,
E=2x106 кгс/см2.
|
Имеем четвёртую схему нагружения. Находим
величину предельно допустимой нагрузки. Принимаем условие - нагрузка под мешками должна быть на ~20 % меньше предельно
допустимой нагрузки. Увеличиваем полученное значение в 2 раза (по количеству труб).
|
| Графоаналитический метод |
Калькулятор |
Графоаналитический метод |
Калькулятор |
|
W
= 42 см3
J
= 147 см4
F1max
= 305 кг
y
= 70 мм |
W
= 42,29 см3
J
= 148 см4
F1max
= 310,12 кг
у
= 68,4 мм |
W
= 20 см3
J
= 55 см4
F3max
= 768 кгc
Fsym
(80% F3max) = 1228,8 кгс.
Кол-во
мешков - 24 шт.
F
= 307 кг
y =
77 мм. |
W
= 19,97 см3
J
= 54,9 см4
F3max
= 769,2 кг
Fsym
(80% F3max) = 1230,7 кгс.
Кол-во
мешков - 24 шт.
F
= 307,7 кг
у
= 72 мм |
Справочная информация для расчета балки на прогиб
Допускаемыми напряжениями называют максимальные значения расчетных напряжений, которые могут быть допущены в опасном сечении,
при обеспечении необходимой в условиях эксплуатации надежности работы детали.
Таблица 1
- Допускаемое напряжение при изгибе сталей разных марок под воздействием нагрузки (постоянной, переменной, знакопеременной) после различных видов термообработки
| Материал |
Термическая обработка |
Допускаемое напряжение при изгибе, кгс/см2 |
| нагрузка статическая |
переменная |
знакопеременная |
| |
|
Сталь 15
|
Нормализация |
950
|
800
|
600
|
| Цементация с закалкой в
воде и отпуск на твердость HRC 56 - 62 |
1500
|
1150
|
800
|
|
Сталь 35
|
Нормализация |
1350 |
1100 |
800 |
| Улучшение |
2100
|
1550
|
1000
|
| Закалка в воде и отпуск на твёрдость HRC 33-43 |
2700 |
2000 |
1350 |
Сталь 45 |
Отжиг |
1350 |
1100 |
800 |
| Нормализация |
1550 |
1250 |
950 |
| Улучшение |
2200 |
1750 |
1300 |
| Закалка в воде и отпуск на твёрдость HRC 38-48 |
3000 |
2200 |
1450 |
Сталь 20X |
Нормализация |
1500 |
1150 |
800 |
| Улучшение |
2100 |
1550 |
1000
|
| Цементация с закалкой в масле и отпуск на твёрдость 56-62 |
3000 |
2200 |
1400 |
Сталь 40X |
Отжиг |
1800 |
1400 |
1000 |
| Улучшение |
2700 |
2000 |
1350 |
| Закалка в масле и отпуск на твёрдость HRC 37-41 |
4300 |
3100 |
1900 |
| Закалка в масле и отпуск на твёрдость HRC 46-50 |
5100 |
3700 |
2300 |
12XH3 |
Нормализация |
1900 |
1400 |
950 |
| Цементация с закалкой в масле и отпуск на твёрдость HRC 55-61 |
3200 |
2400 |
1550 |
Перевод единиц: 1 кгс/см2 = 98,0665 кПа
Таблица 2
- Модуль упругости различнх материалов
|
Материал
|
Модуль упругости (модуль Юнга)
Е·105,
кгс/см2
|
|
Алюминиевый сплав
литейный
Дюралюмин после отжига
при 370 0С
В95-ТI
-
АК8-TI,
Д16-Т -
АМг6
-
|
6.7 - 7.2
7 - 7.5
7
7.2
6.8
|
|
Бакелит (без наполнителей)
|
0.2 - 0.6
|
|
Бронза фосфористая
катанная
|
11.5
|
|
Титановый сплав
- ВТ6
|
11.2
|
|
Железо Армко
сварочное
|
21
16 - 20
|
|
Магниевые сплавы -
ВМ65-I, МА2-I
|
4.2
|
|
Латунь холоднотянутая
|
9.1 - 9.9
|
|
Медь холоднотянутая
прокатная
|
11 - 13
|
|
Монель-металл
|
17.6
|
|
Свинец
|
1.7
|
|
Стальное литьё
|
17.5
|
|
Стали углеродистые
|
20 - 21
|
|
Стали хромоникелиевые
-
30ХГСНА
-
12Х2НВФА
|
20 - 21
19.5
20
|
|
Стекло
|
4.9 - 6.3
|
|
Текстолит
|
0.6 - 1
|
|
Целлулоид
|
0.17 - 0.2
|
|
Цинк катанный
|
8.4
|
|
Чугун
серый, белый
ковкий
|
15.5 - 16
до 15.5
|
|
Никель |
21 |
|
Вольфрам |
36 |
|
Золото |
1.6 |
|
Нейлон |
0.5 |
|
Кость |
2 |
|
Стеклопластик - АФ -10В |
2.44
|
Модуль упругости (модуль Юнга [Томас
Юнг, 1773 - 1829] ) - коэффициент
пропорциональности между F/S (усилие/площадь
поперечного сечения) и относительным
удлинением (растяжением) dL/L, полученный для
определённого материала.
web-сайт
ГРАФОАНАЛИТИЧЕСКИЕ СИСТЕМЫ
Контактная информация (e-mail): nomogramka@gmail.com
Copyright© 2005-2022 г. Все права защищены.
